*[Mano의 컴퓨터 시스템 구조 3판]의 공부할겸 요약한 내용입니다.
이진 소수점
- 컴퓨터에서 +부호는 0, -부호는 1로 표기된다.
- 이진 소수점의 위치는 소수 부분이나 정수 부분 또는, 정수-소수 함계 표시하기 위해 필요하다.
- 레지스터 내에서 이진 소수점의 위치를 표기하는 두가지 방법: 고정 소수점 표현, 부동 소수점 표현
고정 소수점 표현(Fixed-Point Representation)
이진 소수점은 언제나 고정된 위치에 존재한다.
(1) 분수를 표현하기 위해서 레지스터의 맨 왼쪽에 두는 것
(2) 정수값을 표현하기 위해서 레지스터의 맨 오른쪽에 두는 것
3가지 정수 표현 방법
(1) 부호 절대값 표현 ex) +14: 0 0001110, -14: 1 0001110
(2) 부호화된 1의 보수 표현 ex) +14: 0 0001110, -14: 1 1110001
(3) 부호화된 2의 보수 표현 ex) +14: 0 0001110, -14: 1 1110010
산술 가산(Arithmetic Addition)
*음수는 2의 보수로 변환
*음의 몫은 2의 보수로 표기 된 것이다.
Addition Rules(1) 부호를 포함한 두 수를 더한다.(2) 부호에서 최종 Carry는 버린다.
산술 감산(Arithmetic Subtraction)
*음수는 2의 보수로 변환
*음의 몫은 2의 보수로 표기 된 것이다.
Subtraction Rules
(1)감수를 부호에 포함해서 2의 보수로 변환 후, 부호에서의 최종 Carry는 버린다.
(+-A) - (+B) = (+-A) + (-B)
(+-A) - (-B) = (+-A) + (+B)
오버플로(Overflow)
(n 자리 수) + (n 자리 수)가 (n+1 자리 수)가 되는 경우이다.
양수끼리 더하거나 음수끼리 더할 경우 오버플로가 발생할 수 있다.
부호를 중심으로 Carry-in인과 Carry-out 값이 같지 않으면 오버플로 조건이 된다.
ex) (+11) + (+11) = +110 >> 오버플로 발생
십진수 고정 소수점 표현 - BCD 방식의 예
각 10진수 한자리 수는 4F/Fs를 필요로 한다.
+는 0000으로, -는 1001으로 각각 4비트를 차지한다.
십진수와 BCD표가 이진수 사이에 변환이 불필요하나, BCD 방식은 회로가 복잡하고 저장공간 낭비가 크다.
ex) -4385를 BCD로 표기할 경우...
-: 1001
4: 0100
3: 0011
8: 1000
5: 0101
따라서, 1001 0100 0011 1000 0101이 된다.
부동 소수점 변환(Floating-Point Representation)
연산이 복잡하고, 시간이 많이 소요된다.
연산은 H/W나 S/W Sub-routine으로 처리한다.
매우 크거나 작은 수를 표현할 때 용이하다. ex) +0.1866468 x 10^150
m x r^e m: 가수, r: 진수, e: 지수
부동 소수점 표기법은 두 부분으로 구성이 된다.
(1) m = signed, 정규화된 fixed-point number 표현
(2) e = 이진 소수점 위치 표현
*정규화 상태로 표현한다.
(1) m 부분 중 숫자의 MSB가 0이 되지 않도록 하는 것이다.
(2) 숫자의 높은 정밀도를 제공하기 위해 사용한다.
ex) 이진수 (+101.11): m x 2^e = +(.1011100) x 2^+(3)= 0(.1011100) x 2^0(0000011)
Gary Code
증감 시 오직 1비트값만 바뀐다.
각 자리수의 중요도가 같다. 즉, MSB, LSB가 없다.

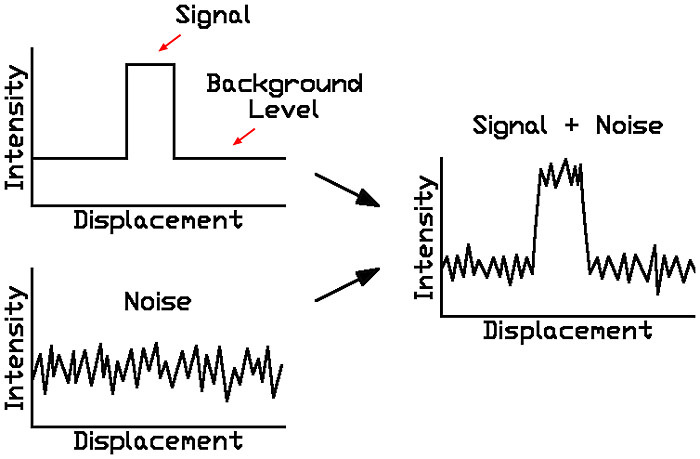
에러 검출 코드(Error Detection Codes)
- 이진 정보 전송 시, 외부 소음 등에 의해 전송 내용이 변조되는 것을 발견하기 위해서 필요하다.
- 가장 일반적인 에러 검출 방법은 패리티 비트를 사용하는 것이다. > 두 비트가 동시에 에러면 에러 검출이 불가능하다.
패리티 비트
Binary Message에 1비트를 추가하여 전체 1의 개수를 짝수로 만들거나, 홀수로 만든다.
이때, 추가되는 1비트를 패리티 비트라고 한다.
짝수 패리티 기법 (Even-parity method)
패리티 비트를 포함한 메세지 전체의 1의 개수가 짝수가 되도록 하는 방법이다.
ex) 1000011은 1이 3개 있기 때문에
짝수 패리티 기법에 의해 1을 추가한다.
따라서, 11000011
홀수 패리티 기법 (Odd-parity method)
패리티 비트를 포함한 메세지 전체의 1의 개수가 홀수가 되도록 하는 방법
ex) 1000011은 1이 3개 있기 때문에
홀수 패리티 기법에 의해 1을 추가하지 않고 0을 추가한다.
따라서, 01000011 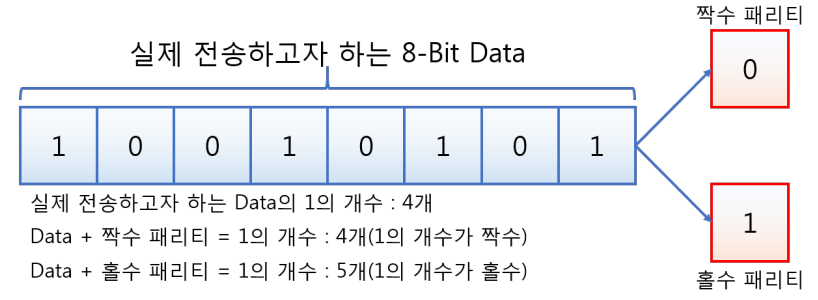
패리티 발생기(Generator)/검사기(Checker)
(1)송신 측에는 패리티 발생기를, 수신 측에는 패리티 검사기를 설치해야한다.
(2)패리티 발생기 출력은 패리티 비트
(3)패리티 검사기 출력은 에러가 없을 시 0, 에러 발생 시 1이다.
(4)홀수 개 비트들의 에러 발생 시에만 에러 검출이 가능하다.
따라서, 이 시스템의 에러 검출 효율성은 50%이다.
(5)에러가 발생한 비트들의 위치는 판별이 불가하다.
*짝수 패리티 발생기 설계 예시

'컴퓨터 구조' 카테고리의 다른 글
| [컴퓨터 구조] 마이크로 연산 (0) | 2022.05.05 |
|---|---|
| [컴퓨터 구조] Register 전송 (0) | 2022.05.04 |
| [컴퓨터 구조] Memory와 숫자 표현 (0) | 2022.04.11 |
| [컴퓨터 구조] Digital 부속품 요약 (0) | 2022.04.07 |
| [컴퓨터 구조] Circuits 특성과 Flip-Flop (0) | 2022.04.06 |



